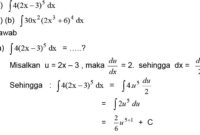Contoh Soal Analisis dalam Matematika
Analisis adalah cabang matematika yang berfokus pada perubahan, limit, dan kes continuidad. Analisis digunakan untuk mempelajari berbagai fenomena alam, termasuk gerak benda, perubahan suhu, dan pertumbuhan populasi.
Berikut ini beberapa contoh soal analisis matematika:
- Menentukan limit fungsi. Limit fungsi adalah nilai yang didekati fungsi saat argumen mendekati suatu nilai tertentu. Misalnya, limit fungsi $$f(x) = x^2$$ saat $$x$$ mendekati 0 adalah 0.
- Menentukan turunan fungsi. Turunan fungsi adalah laju perubahan fungsi terhadap argumennya. Misalnya, turunan fungsi $$f(x) = x^2$$ terhadap $$x$$ adalah $$2x$$.
- Menentukan integral fungsi. Integral fungsi adalah luas daerah di bawah kurva fungsi. Misalnya, integral fungsi $$f(x) = x^2$$ terhadap $$x$$ dari 0 sampai 1 adalah $$1/3$$.
Aplikasi Analisis dalam Sains dan Teknik
Analisis digunakan dalam berbagai bidang sains dan teknik, termasuk:
- Fisika: Analisis digunakan untuk mempelajari gerak benda, gaya, dan energi. Misalnya, persamaan gerak Newton $$F = ma$$ dapat diturunkan menggunakan analisis.
- Kimia: Analisis digunakan untuk mempelajari reaksi kimia dan sifat zat. Misalnya, hukum kekekalan massa dapat diturunkan menggunakan analisis.
- Biologi: Analisis digunakan untuk mempelajari pertumbuhan populasi, penyebaran penyakit, dan evolusi. Misalnya, persamaan Lotka-Volterra dapat digunakan untuk memodelkan pertumbuhan populasi.
- Teknik: Analisis digunakan untuk merancang jembatan, bangunan, dan mesin. Misalnya, analisis struktur dapat digunakan untuk memastikan bahwa jembatan cukup kuat untuk menahan beban yang diterapkan padanya.
Tantangan dalam Analisis
Analisis adalah bidang matematika yang menantang, tetapi juga sangat bermanfaat. Beberapa tantangan dalam analisis meliputi:
- Kalkulus: Analisis didasarkan pada kalkulus, yang merupakan cabang matematika yang berfokus pada limit, turunan, dan integral. Kalkulus dapat menjadi topik yang sulit dipahami bagi sebagian orang.
- Abstraksi: Analisis adalah cabang matematika yang sangat abstrak. Ini dapat membuat sulit untuk memahami konsep-konsep analisis dan menerapkannya pada masalah dunia nyata.
- Aplikasi: Analisis dapat digunakan untuk memecahkan berbagai masalah dunia nyata, tetapi tidak selalu mudah untuk melihat bagaimana analisis dapat digunakan untuk memecahkan masalah tertentu.
Sampai jumpa kembali di artikel lainnya.